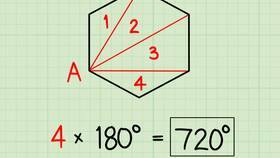
Правильный треугольник, также известный как равносторонний треугольник, обладает особыми свойствами, которые делают его фундаментальной фигурой в геометрии. Одним из ключевых свойств является сумма его внутренних углов.
Содержание
Основное свойство суммы углов треугольника
Для любого треугольника, включая правильный, сумма внутренних углов всегда равна 180 градусам. Это фундаментальное свойство евклидовой геометрии.
| Тип треугольника | Сумма углов |
| Правильный (равносторонний) | 180° |
| Равнобедренный | 180° |
| Разносторонний | 180° |
Особенности правильного треугольника
- Все три стороны равны по длине
- Все три угла равны между собой
- Каждый угол равен 60 градусам (180° ÷ 3)
- Обладает максимальной симметрией среди треугольников
Доказательство суммы углов
Геометрический метод
- Проведите прямую линию, параллельную одной из сторон треугольника
- Используя свойства параллельных линий и секущей, покажите равенство углов
- Убедитесь, что три угла вместе образуют развернутый угол (180°)
Алгебраический метод
Для правильного треугольника с углами α, β, γ:
- α = β = γ (по определению правильного треугольника)
- α + β + γ = 180° (общее свойство треугольников)
- 3α = 180° ⇒ α = 60°
Практическое значение
Знание суммы углов правильного треугольника имеет важные приложения:
| Архитектура | Проектирование устойчивых конструкций |
| Инженерия | Расчеты механических систем |
| Компьютерная графика | Построение трехмерных моделей |
| Навигация | Триангуляционные методы |
Заключение
Сумма углов правильного треугольника, как и любого другого треугольника в евклидовой геометрии, всегда составляет 180 градусов. Особенность правильного треугольника заключается в том, что все его углы равны между собой и составляют по 60 градусов каждый. Это свойство делает правильный треугольник идеальной фигурой для многих математических и инженерных расчетов.